A talented person can always improve their lot in society. Of course it helps if you start with a lot of wealth in the first place. As the late, great Denholm Reynholm said "When I started Reynholm Industries, I had just two things in my possession: a dream and six million pounds."
But you must also have luck. You can be born a prince, and have a genius level of intelligence, get the best education and be set to inherit the absolute power of the crown and the huge wealth of a treasury, but a single encounter with the wrong virus can kill you before you do.
Luck, be it an innate property of nature, or the unpredictable result of a huge number of deterministic interactions, is needed to bring and sustain your fortune. But here's the question I wish to address. To what extent can the wealth inequality in our society be explained by chance alone?
Let's make things hard for ourselves and imagine a society of perfect equality in which everyone has the same amount of wealth. Yes, I know this is far-fetched, but humour me for a while and treat it as a fairy tale.
Now imagine that the king decrees all wealth is void, including his own, and everyone must have perfect equality of opportunity. The king locks up all existing forms of wealth in a secret cave and to each person he gives one coin. Possession of one coin is enough to make sure your kingdom will provide you with life's basics of food and shelter, but no more. Your life is austere. The king abdicates and accepts the same austerity.
But the coin is magic. Once a year the owner can toss it and if it comes up heads, a second non-magic coin appears. Those with two coins are now provided with goods and opportunities beyond the basics. Perhaps some coffee or a chance to travel beyond their home town or city and see more of the world. (Let's not worry too much how the kingdom provides this stuff, and as this is a fairy tale let's assume the king left this task to the Genie of Goods and Services as his final act.)
The next year, each person gets to toss their magic coin again. If they get heads, another two non-magic coins appear, doubling their wealth to four coins in total. And if they get tails they just keep whatever they've got.
This process continues. Each year those lucky individuals who get heads double their wealth, that is, the number of coins. After three years, the luckiest people who got heads all three times will have 8 coins (2×2×2), some will have 4 coins (2×2), some will have 2 coins, and a few unfortunate souls will continue to lead a basic existence with just one coin, albeit a magic one. Our initially perfectly equal society has now become somewhat unequal, and all through chance. No skill is involved at all.
If the magic coin is also a fair one and has a 50:50 chance of heads or tails then it is fairly easy to figure out what fraction of the population has 8 coins. The probability of getting one heads is a half, so the probability of getting three heads is ½ × ½ × ½ = ⅛. So one eighth of the population, or 12.5%, will have eight coins. The exact same argument can be made for three tails, so an eighth will have only one coin.
For those with 4 coins, they must have got two heads and one tails. Now this requires a bit more care to understand. The probability of getting a particular sequence, say, heads then heads then tails, or HHT for short, is also one eighth. In fact, any specific sequence of three coins has probability of an eighth. But, there are three sequences that have two heads, HHT, which we've seen, but also HTH and THH. So the probability is three-eighths or 37.5%. Again the same argument can be made for two tails.
So, to summarise, there are only four possible levels of wealth:
- An eighth or 12.5% of the population have 8 coins.
- Three eighths or 37.5% of the population have 4 coins.
- Three eighths or 37.5% of the population have 2 coins.
- An eighth or 12.5% of the population have 1 coin.
If you add these fractions up you get 1 or 100% which means we have indeed accounted for everyone and all possibilities.
After three years, this society is still quite an equal one, and there are only four levels of wealth because there are only four possible outcomes, so it bears no resemblance to any reality. But let's now imagine we let this go on for a generation, say 30 years.
There are now just over a billion outcomes (2 raised to the power 30), and we can prove something that is not at all intuitively obvious: in a population of about a billion people it is likely that there is one person who got heads every single year. This hyper-lucky person will be a billionaire with their number of coins being 2 raised to the power 30.
Now if you think there is something wrong with this, then it might help to restate it in a more intuition-friendly way: in a population of a billion people, it is fairly likely that one person will experience an event that only has a one-in-a-billion probability.
Further, we can expect about 30 people will have half this wealth because they got 29 heads and one tails. You can understand this because there are 30 sequences in which just one tails can occur, compared to just one sequence that is all heads.
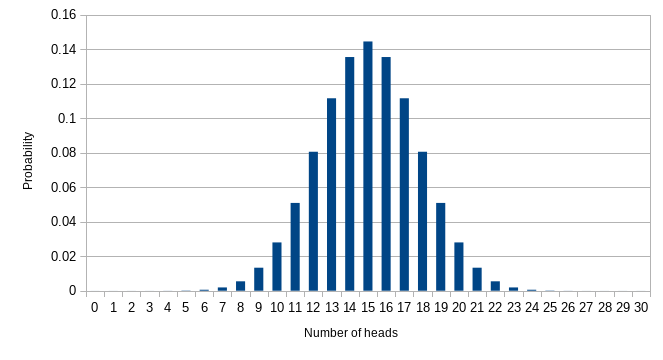
The distribution of wealth from coin tosses is the well-studied binomial distribution that I described in an earlier post on the statistics of political polling. The 'bi' in binomial refers to the fact that there are two outcomes in each coin toss. This graph shows the distribution after 30 tosses, but the profile of the distribution is much the same for any number of tosses, resembling a bell centred on half the number of tosses (the fact it looks like a bell has a significance I'll return to in a future post).
As we saw for three coin tosses above, if you add up all the probabilities on this graph you get 1 which again means we've accounted for all possibilities. But more interesting is the fact that if we add up all the probabilities from 10 to 20 inclusive, then we get 0.96. In other words, 96% of the population will find their number of heads being between 10 and 20 after 30 years. The remaining 4% are split evenly between being either very lucky and wealthy, or very unlucky and poor.
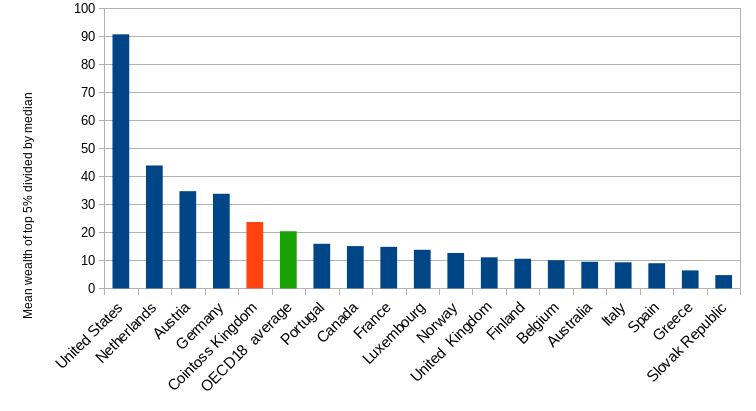
After 30 years of magical coin tossing in our mythical kingdom, we can use the binomial distribution to calculate a statistic that measures the wealth inequality. First we work out the average (specifically the mean) wealth of the wealthiest 5% of people in the kingdom. Next we work out the median, which is the wealth that divides the kingdom into two equally sized groups. Our measure of inequality is to divide the average of the top 5% by the median. Without boring you with the numerical finagling of the binomial distribution, the result for Cointoss Kingdom is 24.
So what? Well, we can now compare this with the same statistic produced for our own world by the OECD. This graph shows data from Table 6.3 in their In It Together report and, as you can see, Cointoss Kingdom sits very close to the OECD average.
In summary, starting with each individual having the same wealth and applying a simple scheme with perfect equality of opportunity, determined only by chance — or luck, if you prefer — it is possible to produce observed levels of real wealth inequality.
But, that said, Cointoss Kingdom's distribution of wealth is quite unlike a real society because it has most people on middle wealth and almost no-one on zero or low wealth.
An interesting subsequent question, which I'll turn to in the next blog post, is can a similar luck-only model be used to produce the kind of distribution that we see in reality? And can we do it without invoking magic coins and genies?