This morning I was delighted to come across this story about a startling correlation between the number of mobile phone masts in an area and the birth rates. Given the talk about mobile phone signals and health (for which there is no good evidence), even I was tempted into thinking "oooh, mobile phone masts get people horny or more fertile".
But of course, it's actually quite obvious when
you consider what data is being analysed. Lots of mobile phone masts
in an area just means that lots of people live in that area and lots
of people means lots of births. Hence there's a correlation between
the number of masts in an area and the number of births.
Looking at the data, a more interesting analysis would be to take
the births per thousand people and correlate that with the number of
masts per thousand people in each area. My guess is that there might
be a much weaker correlation, but it may still show some interesting
effects. For example, is the birth rate higher in areas with greater
population density in which more phone masts are erected? Is there
more NIMBYism against phone masts in prosperous areas with lower
housing density?
This housing phenomenon must be an age-old one and mobile phone masts are just a new proxy for it. I recently researched the history of the defunct mining village of Mavis Valley and in the 1901 census data (which, alas, isn't freely available on the web), I found that 49% of the village's population was under 15. At first I thought "wow, compare that with our aging population these days", but then I realised that the percentages for my own street - about 20 three and four bedroom houses built in 1995 - had a very similar percentage of under 15s. Sure enough, when I checked, I found that Mavis Valley had undergone a major expansion in the decade before the census and so young couples had moved into the new houses and started breeding.
A magnet for numerology and pseudo-science (i.e.
nonsense) is the sunspot number time series, which I spent three years
of my life studying. Your eye and brain might be attracted by the
graph in this example:
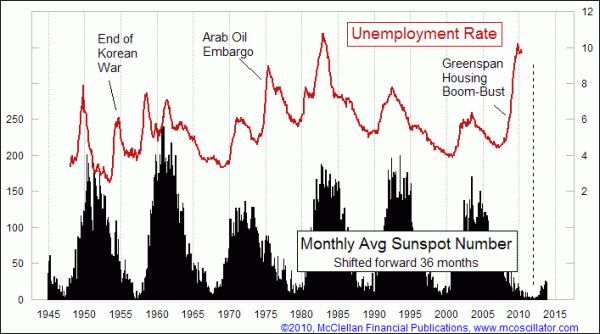 But look more
closely and critically and ask yourself these three questions:
But look more
closely and critically and ask yourself these three questions:
- How many graphs did the author compare with sunspot number before choosing to blog about this one?
- A time shift of 3 years was needed to expose the correlation and no data before 1947 is included - is there a reason for these choices other than to improve the correlation?
- There are 10 distinct unemployment peaks but only 4 of them line up with peaks in sunspot number, the other 6 don't. Are you convinced by a sample of 10 data points of which 6 do not agree with hypothesis proposed?